ベクトル演算を理解する

ベクトル演算は3Dグラフィックス,物理演算およびアニメーションにとって基本であり,さらに深く理解することでUnityを最大限活用するのに役立ちます。以下で主要な演算および活用できる多くの場面に関しての提案をまとめます。

加算

二つのベクトルが互いに足しあわされるとき,結果はもとのベクトルを次から次への “ステップ” とみなすのと同じです。二つのパラメータの順番はどちらにせよ同じになるので影響がないことに留意下さい。

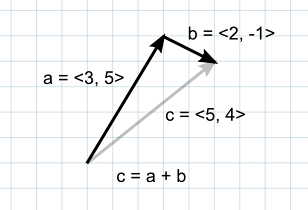
もし最初のベクトルを空間上の点とした場合,2つ目のベクトルはその位置からのオフセットまたは “ジャンプ” とみなすことが出来ます。例えば,地面から5ユニット上の位置を見つけるためには次の計算を用いることが出来ます:-

 var pointInAir = pointOnGround + new Vector3(0, 5, 0);

もしベクトルが力を表す場合,より直感的な捉え方は向きや大きさです（大きさは力の大きさです）。二つのベクトルを足すことは力の合成と同じです。この考え方は別のコンポーネントで同時に加えるときに便利です（例えば,正面に向うロケットが横風の影響を受けているかもしれません）。

減算

ベクトルの減算をもっとも良く使う場面はひとつのオブジェクトから別のオブジェクトへの向きと距離を出すためです。減算の場合は二つのパラメータの順番は 影響がある ことに留意下さい。

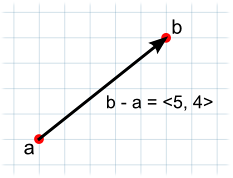
// The vector d has the same magnitude as c but points in the opposite direction.
var c = b - a;
var d = a - b;

数字については,負の値のベクトルを足すのはその正の値のベクトルを減算するのと同じです。

// These both give the same result.
var c = a - b;
var c = a + -b;

負の値のベクトルはもとと同じ大きさであり,同一線分上に沿いますが,全く逆の方向となります。

スカラー乗算および除算

ベクトルについて議論するとき,普通の数字（例えば浮動少数点の値）をスカラーとみなすことが通常です。この意味は,スカラーはひとつの “スケール” または大きさしかありませんが,ベクトルには大きさと向きがあります。

ベクトルにスカラーを乗算すると,元のベクトルと同じ方向を向くベクトルが得られます。しかし,新しいベクトルの大きさは元の大きさにスカラーの値を乗算した値となります。

同様に,スカラーの除算は元のベクトルの大きさをスカラーで割ります。

これらの演算はベクトルが動作のオフセットまたは力を表現するときに便利です。これによりベクトルの向きを変えることなくの大きさを変更できます。

あるベクトルが自身の大きさにより除算されると結果は大きさが1のベクトルとなり,これは正規化ベクトルと呼ばれています。もし成果ベクトルにスカラーを乗算すると,結果の大きさはスカラーの値と同じになります。これは力の向きが一定でありながら強さが制御できるときに便利です（例えば,車の車輪はつねに前に進みますが,強さはドライバーにより制御されます）。

内積

内積は二つのベクトルによりスカラーを返します。このスカラーは二つのベクトルの大きさを乗算したもの,およびベクトルのなす角のコサインと等しくなります。両方のベクトルが正規化されているとき,コサインは本質的に最初のベクトルが二つめのベクトルの向きに進んでいるかを表します（あるいはその逆もあり,パラメータの順番は影響ありません）。

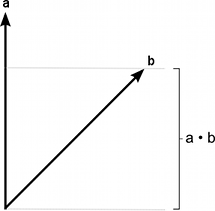
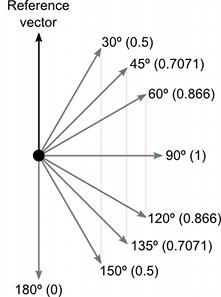
角度をもとにして,対応するコサインを計算機により見つけることは容易です。しかし,下図のようにいくつかの主なコサインの値を直感的に理解することが役に立ちます:

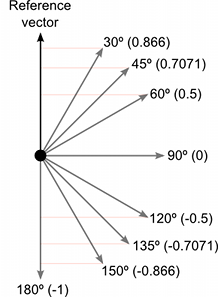
内積はとてもシンプルな演算であり,Mathf.Cos関数のまたはいくつかのケースではベクトルの magnitude 演算の代わりに使用でｓきます。（まったく同じではありませんが,場合によっては得られる効果は同じです）。しかし,内積の関数を利用したほうが要するCPU時間が短く,このために価値の高い演算となります。

外積

この他の演算は 2D および 3D ,あるいはより高次元ベクトルのでも定義ができます。一方で対照的に,外積は,3Dベクトルでしか意味をなしません。二つのベクトルをもとに,別のベクトルを結果として出力します。

結果ベクトルは二つの入力ベクトルに対して垂直になります。“左手の法則” を覚えることで,入力ベクトルの順番による出力ベクトルの向きを判断することが出来ます。もし最初のパラメータが手の親指,二つめのパラメータが人差し指,そして結果は中指の方向を指します。もしパラメータの順番が逆になると結果のベクトルは正反対の向きで,ただし同じ大きさとなります。

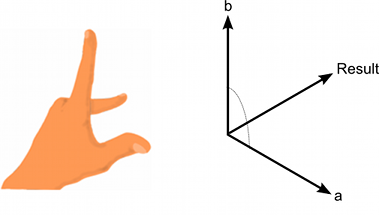
結果の大きさは入力ベクトルの大きさを乗算して,さらにそれらがなす角のサインを乗算したものとなります。サイン関数で役立つ値を以下で示します:

外積は,いくつかの便利な情報を返り値に合成するため複雑に感じられるかもしれません。しかし,内積と同様に数学的にとても効率的であり,これを使用しなければ遅い超越関数に依存するコードを最適化することが出来ます。