メッシュの構造

メッシュは,固形のオブジェクトのようにに見せるために,3D空間に並べられた三角形から構成されています。三角形は3つの角の点,すなわち頂点により定義されます。Mesh クラスでは,すべての頂点はひとつの配列に格納されていて,各々の三角形は頂点配列のインデックスにあたる3つの整数により指定されます。三角形はさらに一つの整数の配列として集められます。この整数はこの配列の最初から3つごとにグルーピングされるため,要素0,1,および 2 は最初の三角形を定義し,二つ目の三角形は3,4,および 5,と続いていきます。任意の頂点は好きなだけ三角形を定義するのに再利用できますが,口述するように,考慮してそれは避けるべき理由がいくつかあります。

ライティングと法線

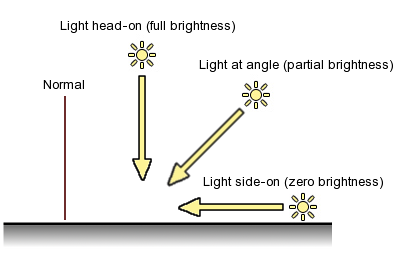
三角形はオブジェクトの基本図形を定義するのに十分ですが,大部分のケースではメッシュを表示するのには追加の情報が必要です。オブジェクトがライティングにより正しくシェーディングされるためには,法線ベクトルは各頂点のために提供する必要があります。法線は外向きに向かうベクトルであり,メッシュ表面に対して垂直に各頂点の位置から出ています。シェーディング計算において,各頂点の法線は入射するライト,これもまたベクトル,の方向と比較されます。もし二つのベクトルが完全に平行である場合,平面はその点において真正面からライトを受け取り,ライトの明るさのすべてはシェーディングに使用されます。法線ベクトルに対して真横から入射する光の場合,平面はその点においてまったく照らされることがありません。一般的にライトは法線とある角度で入射するため,その入射角によって完全な明るさと完全な暗さとの間の値となります。

メッシュは三角形から構成されているため,角の法線は三角形の平面に対して垂直であるように感じるかもしれません。しかし,法線は実際には三角形に渡って補間されて,角の間の平面の中間位置に方向が割り当てられます。もし3つの法線がすべて同じ方向を指す場合,三角形は均等に全面がライティングされます。別の三角形を均等にシェーディングされる効果は,そのエッジがはっきり際立つことになります。これはキューブ,または尖ったエッジの固体のようなモデルにとっては必要なことですが,カーブのある表面をを近似するようなスムーズなシェーディングを作成する場合には法線の補間が必要です。

綺麗なエッジを表示するには,頂点を各エッジ付近で二重化することが必要で,隣接する二つの三角形はそれぞれ別の法線が必要であるためです。 カーブのある表面では,頂点はエッジに沿って共有すればよいのですが,シェーディングされた法線の最適な向きを決定するにはかなりの勘が必要であることが多いです。法線は単に三角形を囲む表面の法線の平均であるかもしれません。しかし,球のようなオブジェクトでは,法線は球の中心から外向きに向かっているべきです。

Mesh.RecalculateNormalsをコールして,メッシュ物体の “意味” について仮定を置くことで,Unityが自動的に法線の方向を算出させるようにできます。三角形により共有される頂点がスムーズな表面を表し,二重の頂点ははっきりしたエッジを示すと仮定します。これは多くのケースで悪い推定ではありませんが, 表面がスムーズであるにも関わらず二重化する必要があるいくつかのテクスチャの状況ではRecalculateNormals は失敗します。

テクスチャリング

ライティングに加えて,モデルは一般的にテクスチャを活用して,平面上にディテールを作成することが出来ます。テクスチャは伸縮可能なゴムのシートにプリントしたイメージのようです。各三角形メッシュで,テクスチャイメージの三角形領域が定義されて,そのテクスチャ三角形は伸縮されて メッシュ三角形に合うように “ピン付け” されます。これを機能させるためには,各頂点はピン付けするイメージ位置の座標を格納する必要があります。これらの座標は二方向であり,0 - 1 の範囲でスケールされます（0 はイメージの左／下を表し1は右／上を示します）。この座標を3D空間のデカルト座標と混同しないために,これらはよく使用されるX, YをさけてU,Vで指定され,UV座標と呼ばれます。

法線のように,テクスチャ座標は各頂点に固有のものであり,このため純粋にエッジにわたって異なるUV座標を得るために,頂点を二重化したい状況があります。明らかな例としては,二つの隣接する三角形が連続しないテクスチャ イメージを使用する（例えば顔テクスチャにある目など）場合などです。さらに完全に閉じた体積であるオブジェクトは “シーム” が必要で,そこではテクスチャの領域が一周して互いに繋がっています。シームの片側のUV座標の値は反対側と異なる値になります。