ランダムなゲームプレイ要素の追加
ランダムに選ばれたアイテムまたは値は多くのゲームで重要です。本項ではUnityの内蔵 random 関数を使用して良くあるゲーム システムを実装する方法を取り上げます。
配列からランダムなアイテムを選択する
ランダムな配列要素を選ぶことはランダムな整数をゼロから配列の最大のインデックス値(配列の長さから1を引いた値)を選ぶことに要約できる。これは内蔵の Random.Range 関数により実現できます:-
var element = myArray[Random.Range(0, myArray.Length)];
Random.Range が最初の引数の含むけれども二つめの引数は除かれるため,myArray.Lengthとすることが正しいことに留意して下さい。
異なる発生確率をもったアイテムを選択する
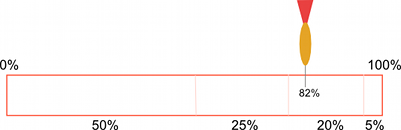
アイテムをランダムに選択しなければいけないが,あるアイテムは他よりも可能性が高い場合があります。例えば,NPC キャラクターはプレイヤーに遭遇したときにいくつかの反応を示す可能性があります:-
- 50% の確率で親しみやすい挨拶
- 25% 確率で逃走
- 20% 確率で急な攻撃
- 5% 確率でお金をプレゼント
これらの異なる結果を分割した紙切れで表現することができて,各々の切れ端は紙切れの全長の一部を占めるとします。その占める長さが選択される結果の確率に相当します。選択を行うことは紙切れの長さ上の任意の点を選んで(例えばダーツを投げるように),どの切れ端にあたるか確認することに相当します
スクリプトの中では紙切れは実際には float の配列で,各々のアイテムに異なる確率を順に格納しています。ランダムな点は Random.valueを全ての float の合計に掛け算することで得られます(足して 1 になる必要はなく,重要なことは異なる値の相対的な長さ)。点がどの配列要素に “入っているか” 調べるために,点の値が最初の要素の値より小さいか比較します。それであれば選択されるのは最初の要素です。そうでなければ,最初の要素の値を点の値から引き算して,それを二つめの要素の値より小さいか比較する,などを繰り返して最終的に正しい要素を見つけます。コードでは次のようになるはずです:-
function Choose(probs: float[]) {
var total = 0;
for (elem in probs) {
total += elem;
}
var randomPoint = Random.value * total;
for (i = 0; i < probs.Length; i++) {
if (randomPoint < probs[i])
return i;
else
randomPoint -= probs[i];
}
return probs.Length - 1;
}
最後の return ステートメントが必要である理由は Random.value は1の値を返す可能性があるためだということに留意して下さい。このケースでは,検索はどこでもランダムな点を見つけることが出来ません。次の行を変更して,
if (randomPoint < probs[i])
…値を <= 記号に変更することで余分な return ステートメントを回避できますが,確率が 0 の場合でもアイテムを選択することも許容してしまいます。
リストをシャッフルする
よくあるゲーム システムは知られたアイテムのセットから選択するけれどもランダムな順番で訪れるというものです。例えば,カードの山は一般的にシャッフルして予想できる順番とならないようにします。アイテムを配列でシャッフルするためには,各々のアイテムを参照して,他のランダムな配列インデックスの要素と入れ替えることが出来ます。
function Shuffle(deck: int[]) {
for (i = 0; i < deck.Length; i++) {
var temp = deck[i];
var randomIndex = Random.Range(0, deck.Length);
deck[i] = deck[randomIndex];
deck[randomIndex] = temp;
}
}
繰り返しなしでアイテムのセットから選択する
良くある作業は,アイテムをセットからランダムに選択して,繰り返し同じものを一回以上選択しないようにするということです。例えば,一定数のNPC キャラクターをランダム位置で生成したけれども,ひとつのNPC だけがある位置で生成されるようにしたい場合があります。これは順番にアイテムを反復して,各々について選択したセットに追加するかどうかランダムな判断を行います。各々のアイテムを参照するたび,それが選択される確率は,まだ必要なアイテムの数をまだ選べる数で割ったものです。
サンプルとして,10 個の生成点が利用可能であるけれども,5 個のみから最初のアイテムが選択される確率は 5 / 10 または 0.5です。もし,それが選ばれた場合,二つめのアイテムが選ばれる確立は 4 / 9 または 0.44 (すなわち,4 個がまだ必要で,9 個からまだ選べます)。これを,セットが必要な 5 個のアイテムを含むまで繰り返します。次のようなコードによりこれを実現できます:-
var spawnPoints: Transform[];
function ChooseSet(numRequired: int) {
var result = new Transform[numRequired];
var numToChoose = numRequired;
for (numLeft = spawnPoints.Length; numLeft > 0; numLeft--) {
// Adding 0.0 is simply to cast the integers to float for the division.
var prob = numToChoose + 0.0 / numLeft + 0.0;
if (Random.value <= prob) {
numToChoose--;
result[numToChoose] = spawnPoints[numLeft - 1];
if (numToChoose == 0)
break;
}
}
return result;
}
選択がランダムであるにも関わらず,選択されたセットのアイテムは最初の配列と同じ順序であることに留意して下さい。もしアイテムが順番に一回づつ使用されるとしたら,順番によって予想可能となってしまうため,配列を使用する前にシャッフルする必要があるかもしれません。
空間におけるランダムな点
立方体の体積におけるランダムな点は,Vector3 の各々のコンポーネントを Random.valueにより返される値でセットすることで選択できます :-
var randVec = Vector3(Random.value, Random.value, Random.value);
これにより辺の長さが 1 単位である立方体の中の点が返されます。立方体を拡大/縮小するにははベクトルのX ,Y ,Z 要素を希望する辺の長さに掛け算するのみです。もし軸のひとつがゼロにセットされる点はひとつの平面上に置かれます。例えば,ランダムな地点を “地面” から選ぶ必要がある場合は, X, Z をランダムに選択して, Y はゼロ にセットすることになります。
体積が球である場合(すなわち,原点から一定の半径に含まれるランダムな点が必要な場合), Random.insideUnitSphere を希望の半径に掛け算できます:-
var randWithinRadius = Random.insideUnitSphere * radius;
もし結果のベクトルの要素のひとつをゼロにしても, 円の中のランダムな点を正しく得ることには「出来ません」。点は確かにランダムで,半径は希望する範囲内にありますが,確率が円周に近づくにつれ大きく偏りができていて,点は不均等に並びます。その状況では変わりに Random.insideUnitCircle を使用すべきです:-
var randWithinCircle = Random.insideUnitCircle * radius;