- Unity User Manual (2020.2 beta)
- スクリプト
- 重要なクラス
- 重要なクラス - Vector
重要なクラス - Vector
ベクトルは数学の基本的な概念で、方向と大きさを表現することができます。ゲームやアプリケーションでは、キャラクターの位置、移動速度、2 つのオブジェクト間の距離など、基本的な特性を表すのに使われます。
ベクトル演算は、グラフィックス、物理、アニメーションなど、コンピュータープログラミングの多くの面で基本となるものであり、Unity を最大限に活用するためには、深く理解することが有効です。
ベクトルは複数の次元で表現することができ、Unity では 2D、3D、4D のベクトルを扱うためにVector2、Vector3、Vector4 クラスを用意しています。 これら 3 種類の Vector クラスは、magnitude などの多くの関数を共有しています。そのため、このページの情報のほとんどは、特に指定がない限り、3 種類の Vector すべてに当てはまります。
このページでは、Vector クラスの概要と、Vector クラスを使ったスクリプティングの一般的な使用方法について説明します。Vector クラスのすべてのメンバーリファレンスは、Vector2、Vector3、Vector4 のスクリプトリファレンスページを参照してください。
ベクトル演算を理解する
加算
2 つのベクトルが互いに足されるとき、結果はもとのベクトルを次から次へと続く “ステップ” のようにみなします。結果はどちらにせよ同じになるので、2 つのパラメーターの順番は関係ありません。
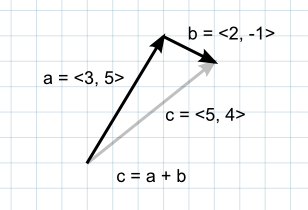
もし最初のベクトルを空間上の点とした場合、2 つ目のベクトルはその位置からのオフセットまたは “ジャンプ” とみなすことができます。例えば、地面から 5 ユニット上の位置を見つけるためには次の計算を用いることができます。
var pointInAir = pointOnGround + new Vector2(0, 5);
もしベクトルが力を表す場合、その向きや大きさ (力の大きさ) と管変える方がより直感的です。2 つの力のベクトルを足すことは、合成した力に等しい値を持つ新しいベクトルと同じです。この考え方は複数のコンポーネントによって同時に力を加えるときに便利です (例えば、前方へ推進するロケットが同時に横風の影響を受ける場合)。
ここでは 2D のベクトルを例に挙げていますが、3D や 4D のベクトルにも同じ概念が当てはまります。
減算
ベクトルの減算は、ひとつのオブジェクトから別のオブジェクトへの向きと距離を出す場合にもっともよく使われます。減算の場合は、2 つのパラメーターの順番は計算結果に 影響を与える ことに注意してください。
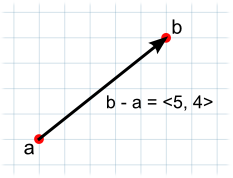
// ベクトル d は c と同じ大きさですが、反対方向に点があります。
var c = b - a;
var d = a - b;
数字については、負の値のベクトルを足すのは、正の値のベクトルを減算するのと同じです。
// これらは両方とも結果は同じです。
var c = a - b;
var c = a + -b;
負の値のベクトルはもとと同じ大きさであり、同一線分上に沿いますが、まったく逆の方向となります。
オブジェクトから別のオブジェクトへの向きと距離
もし空間上の 1 点を別の点から引くと、結果は 1 つのオブジェクトから他方を “指す” ベクトルになります。
// プレイヤーの位置からターゲットの位置を指すベクトルを取得します
var heading = target.position - player.position;
ベクトルはターゲットの方向を指しているだけでなく、その大きさは、2 つの位置の間の距離に等しくなります。ターゲットへの方向を示す “正規化 ”されたベクトルが必要な場合もありますが、距離は固定されています (例えば、砲弾を誘導する場合など)。ベクトルを正規化するには、そのベクトル自体の大きさで割る必要があります。
var distance = heading.magnitude;
var direction = heading / distance; // 正規化された方向になります
大きさ (magnitude) と正規化されたプロパティの両方を別々に使用する場合、両方ともに CPU をかなり消費するため (両方とも平方根計算を含むため)、この方法がより望ましいと言えます。
もし比較のため距離だけが必要な場合 (例えば近接度合いのチェック) は、magnitude の計算をすべて回避できます。sqrMagnitude プロパティは、magnitude の値の 2 乗を求め、magnitude と同じように計算されますが、時間のかかる平方根演算は行われません。magnitude を既知の distance (距離) と比較するのではなく、magnitude の 2 乗を distance の 2 乗と比較できます。
if (heading.sqrMagnitude < maxRange * maxRange) {
// ターゲットは範囲内
}
これは実際の magnitude を比較するよりも遥かに効率的です。
3D で作業をしていると、ターゲットへの “地上の進行方向” が必要になることがあります。例えば、地上に立っているプレイヤーが、空中に浮かんでいるターゲットに近づく必要があるとします。ターゲットの位置からプレイヤーの位置を引くと、結果のベクトルはターゲットに向かって上向きになります。実際に必要なのは、プレイヤーの位置からターゲットの真下の地上の位置までのベクトルです。実際に必要なのは、プレイヤーの位置からターゲットの真下の地上の位置までのベクトルです。これは減算し、Y 座標を 0 にすることで得られます。
var heading = target.position - player.position;
heading.y = 0; // これが地上の進行方向
スカラーの乗算と除算
ベクトルについて議論するとき、通常、普通の数字 (例えば浮動少数点の値) をスカラーとみなします。つまり、スカラーは “スケール” または大きさしかもちませんが、ベクトルには大きさと向きがあります。
ベクトルにスカラーを乗算すると、元のベクトルと同じ方向を向くベクトルが得られます。ただし、新しいベクトルの大きさは元の大きさにスカラーの値を乗算した値となります。
同様に、スカラーの除算は元のベクトルの大きさをスカラーで割ります。
これらの演算はベクトルが動作のオフセットまたは力を表現するときに便利です。これによりベクトルの向きを変えることなくの大きさを変更できます。
あるベクトルをそれ自体の大きさで除算すると、結果は大きさが 1 のベクトルとなり、これは正規化されたベクトルと呼ばれています。もし正規化されたベクトルにスカラーを乗算すると、結果の大きさはスカラーの値と同じになります。これは力の向きが一定で、強さが制御/変更可能な場合に便利です (例えば、車の車輪はつねに前に進みますが、強さは運転者にによって制御/変更されます)。
ドット積
ドット積は 2 つのベクトルを取り、スカラーを返します。このスカラーは 2 つのベクトルの大きさを乗算し、その結果にベクトルの作る角度の正弦を掛けたものと等しくなります。両方のベクトルが正規化されているとき、正弦は本質的に最初のベクトルが 2 つめのベクトルの向きにどれだけ伸びるかを表します (あるいはその逆。パラメーターの順番は影響しません)。
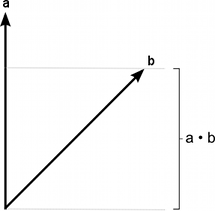
下の図は、参照ベクトルと比較して、どのように様々な角度のベクトルが、1 と –1 の間のドット積を返すかを示しています。
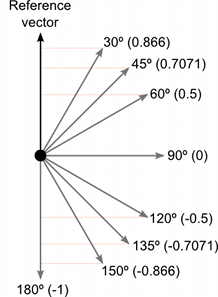
ドット積は、正弦を計算するよりも数学的に単純な演算です。そのため、状況によっては Mathf.Cos 関数やベクトルの magnitude 演算の代わりに使用することができます (全く同じことをするわけではありませんが、同等の効果が得られる場合もあります)。しかし、ドット積関数を計算する方が、はるかに少ない CPU 時間で済むので、価値のある最適化になります。
ドット積は、あるベクトルの大きさが別のベクトルの方向にある量を計算する場合に役立ちます。
例えば、車のスピードメータは一般的にはタイヤの回転速度を計ることで速度を表示します。車は前方向に動いているとは限りません (例えば、横滑りしている)。この場合の動作の一部は車が向いている方向にはならず、スピードメーターによって測定されません。オブジェクトの rigidbody.velocity ベクトルの大きさは全体的な動きの方向の速度を示しますが、前方方向の速度を分離するためには、ドット積を使用する必要があります。
var fwdSpeed = Vector3.Dot(rigidbody.velocity, transform.forward);
当然、方向は好きな方向にすることができますが、この計算では方向ベクトルを常に正規化する必要があります。 結果は速度の大きさよりも正確であるだけでなく、大きさの検出の際の時間のかかる平方根演算も回避されます。
クロス積
クロス積は、3D ベクトルに対してのみ意味を持ちます。2 つの 3D ベクトルを入力として取り、別の 3D ベクトルを結果として返します。
The result vector is perpendicular to the two input vectors. You can use the “left hand rule” to remember the direction of the output vector from the ordering of the input vectors. If the first parameter is matched up to the thumb of the hand and the second parameter to the forefinger, then the result will point in the direction of the middle finger. If the order of the parameters is reversed then the resulting vector will point in the exact opposite direction but will have the same magnitude.

結果の大きさは入力ベクトルの大きさを乗算して、さらにそれらがなす角のサインを乗算したものとなります。サイン関数で役立つ値を以下で示します。
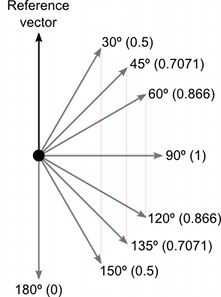
クロス積は、戻り値にいくつかの有用な情報の組み合わせが含まれるため、複雑に見えるかもしれません。しかし、ドット積と同様に数学的に非常に効率的であり、正弦や余弦などの遅い超越関数に依存するコードを最適化するために役立ちます。
法線/垂直ベクトルの計算
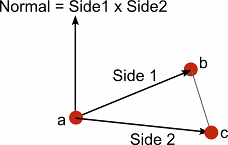
“法線” ベクトル (つまり、平面に垂直なベクトル) は、メッシュ生成の際に頻繁に必要とされ、また経路追跡などにも役立ちます。平面上に 3 つの点、例えばメッシュ三角形の角の点があるとすると、以下のように法線を求めることができます。 - 3 つの点から 1 つを選びます - 他の 2 つのポイントから別々に選んだ点を引きます (結果として 2 つの新しいベクトル、“Side 1” と “Side 2” になります)。 - ベクトル “Side 1” と “Side 2” のクロス積を計算します。 - クロス積の結果は、元の 3 点がある平面に垂直な新しいベクトル、つまり “法線” となります。
Vector3 a;
Vector3 b;
Vector3 c;
Vector3 side1 = b - a;
Vector3 side2 = c - a;
Vector3 normal = Vector3.Cross(side1, side2);
“左手の法則” を使うと、2 つのベクトルをクロス積関数に渡す順番を決めることができます。サーフェスの上側 (そこから、法線が外を向く位置) から見下ろすと、1 つ目のベクトルを時計回りに 2 つ目のベクトルの方に回転させます。
入力ベクトルの順番を逆にすると、結果は正反対の方向になります。
メッシュにとって、法線ベクトルは正規化する必要があります。これは normalized プロパティにより行えますが、もう 1 つのテクニックもときに便利です。また、垂直ベクトルを大きさ (magnitude) で割って正規化することもできます。
float perpLength = perp.magnitude;
perp /= perpLength;
結果的に三角形の面積は perpLength/2 と等しくなります。これはメッシュ全体の表面積を知る必要がある場合、または三角形を相対的な面積にもとづいた確率でランダムに選択したい場合に便利です。