説明
3D 空間での平面の表現
原点から平面への法線ベクトルとの距離によって定義されます。平面は無限に大きな、3 次元空間にある平らな平面であり、空間を二つの半空間と呼ばれるものに分割します。特定の地点がどちらの半空間に存在するか、また平面からどれだけ判定することが容易にできます。壁、床、および他の平らな平面はゲームでよく登場するため、これらのオブジェクトでの数値計算が必要な場合にしばしば役に立ちます。さらに現実には空間が存在しないけれども、あると仮定したほうが便利な場合があります。例えば、スポーツではゴールラインやサイドラインは地上から離れた空間にも存在するものと仮定されるため、要は平面でそのラインを表現できます。
平面がワールド座標の (0, 0, 0) 地点を通過する場合、平面が面する方向を定める法線で定義されます。真正面から平面を見ることを想像すると、可視化することが容易です。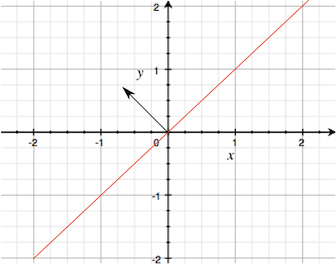
法線がどの向きであるかは重要であり、どの半空間に存在するかを決定づけることに注意してください(すなわち、平面の正の側にあるか反対側にあるか)。平面が (0, 0, 0) 地点を通過しない場合、法線ベクトルに加えて (0, 0, 0) からの距離により定義できます。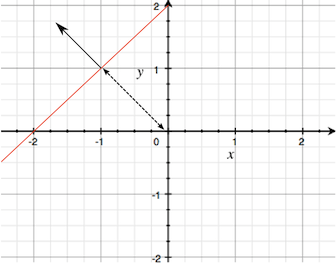
平面を表現する際に、平面上にある三角形の三つの頂点によって定義することもできます。その場合、三角形を正面から見て三角形の頂点を反時計周りにみた場合、法線ベクトルの向きは自分の方に向きます。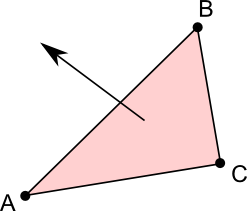 .
.
コンストラクタ
| Plane | 平面を作成します |
Public 関数
| GetDistanceToPoint | 指定したポイントから、平面との距離を返します |
| GetSide | 平面の表がどちらを向いているかを判断します。 |
| Raycast | 平面と交差するレイ |
| SameSide | 2 つのポイントが同じ面側にあるかどうかを判断します。 |
| Set3Points | 3 点の位置を設定して、平面を作成します。このときの 3 点の位置は、上部から見て時計回りで設定されます |
| SetNormalAndPosition | ベクトルの法線と地点により平面を設定します |