Display matrix format and derivation

The display matrix maps the CPU side image to be rendered onto the device's screen, i.e. it maps the CPU side image texture coordinates onto the device's screen coordinates. It is row-major and includes a y-axis flip of the CPU side image texture coordinates (as the image would be upside down when rendered without that y-axis flip). The display matrix is defined as:

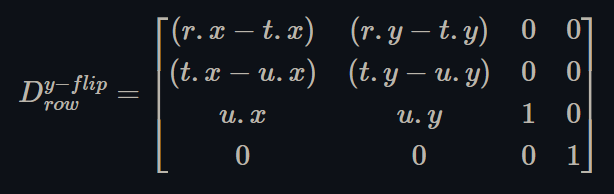
Figure 1. A 4 by 4, row major display matrix that flips the y-axis, named "D row y flip." Row one entries are "r dot x" minus "t dot x", "r dot y" minus "t dot y", 0, 0. Row two entries are "t dot x" minus "u dot x", "t dot y" minus "u dot y", 0, 0. Row three entries are "u dot x", "u dot y", 1, 0. Row four entries are 0, 0, 0, 1
Figure 1 - a row major display matrix that flips the y-axis

The 2D vector "r" corresponds to the right basis vector of the CPU side image coordinates, i.e. the vector that represents the horizontal axis of the image's texture coordinates,

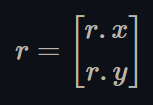
Figure 2. A 2 by 1 vector named "r." The first component is "r dot x". The second component is "r dot y"
Figure 2 - The right basis vector of the image's texture coordinates

The 2D vector "u" corresponds to the up basis vector of the CPU side image coordinates, i.e. the vector that represents the vertical axis of the image's texture coordinates,

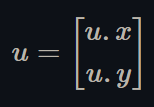
Figure 3. A 2 by 1 vector named "u." The first component is "u dot x". The second component is "u dot y"
Figure 3 - The up basis vector of the image's texture coordinates

The 2D vector "t" corresponds to the offset, or translation, of the above basis vectors, i.e. the location of the origin of the image's texture coordinates,

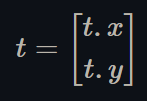
Figure 4. A 2 by 1 vector named "t." The first component is "t dot x". The second component is "t dot y"
Figure 4 - the location of the origin of the image's texture coordinates

Since it is not always obvious what a display matrix is, nor how it is formatted, its derivation is described below if more clarification is needed.

Derive the display matrix

A column-major display matrix that does not flip the y-axis can be defined as:

Figure 5. A 4 by 4, column major display matrix named "D col." Column one entries are "r dot x" minus "t dot x", "r dot y" minus "t dot y", 0, 0. Column two entries are "u dot x" minus "t dot x", "u dot y" minus "t dot y", 0, 0. Column three entries are "t dot x", "t dot y", 1, 0. Column four entries are 0, 0, 0, 1
Figure 5 - a column major display matrix

where "r," "u," and "t" are defined as above in Figures 2, 3, and 4. It is a standard rotation-scale-translation matrix.

1. Use a column major display matrix

Let the following 2D vector be the input texture coordinates of the corresponding vertex shaders, i.e. the texture coordinates of the CPU side image:

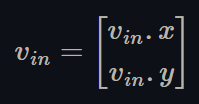
Figure 6. A 2 by 1 vector named "v in." The first component is "v in dot x". The second component is "v in dot y"
Figure 6 - the texture coordinates of the CPU side image

Let the following 2D vector be the output texture coordinates of the corresponding vertex shaders, i.e. the device screen coordinates:

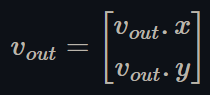
Figure 7. A 2 by 1 vector named "v out." The first component is "v out dot x". The second component is "v out dot y".
Figure 7 - the output device's screen coordinates

To flip the y-axis and find the output texture coordinates with a column-major display matrix, Dcol, the corresponding vertex shaders would have to do:

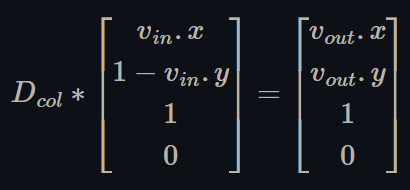
Figure 8. A matrix-vector multiplication equation. It is a 4 by 4 matrix times a 4 by 1 vector, which equals another 4 by 1 vector. The 4 by 4 matrix is "D col" defined in Figure 5. The components of the first 4 by 1 vector are "v in dot x", 1 minus "v in dot y", 1, 0. The components of the second 4 by 1 vector are "v out dot x", "v out dot y", 1, 0.
Figure 8 - use a column major display matrix to transform y-flipped image texture coordinates to screen coordinates

2. Move the y-axis flip into the display matrix

Multiply out the equation from Figure 8 and rearrange the terms, then find the new display matrix such that:

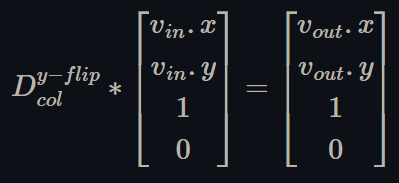
Figure 9. A matrix-vector multiplication equation. It is a 4 by 4 matrix times a 4 by 1 vector, which equals another 4 by 1 vector. The 4 by 4 matrix is a column major display matrix that flips the y-axis called "D col y-flip." The components of the first 4 by 1 vector are "v in dot x", "v in dot y", 1, 0. The components of the second 4 by 1 vector are "v out dot x", "v out dot y", 1, 0
Figure 9 - use a column major display matrix that flips the y-axis to convert image texture coordinates to screen coordinates

This new matrix is defined as:

Figure 10. The definition of the 4 by 4, column major display matrix named "D col y-flip" that was mentioned in Figure 9. Column one entries are "r dot x" minus "t dot x", "r dot y" minus "t dot y", 0, 0. Column two entries are "t dot x" minus "u dot x", "t dot y" minus "u dot y", 0, 0. Column three entries are "u dot x", "u dot y", 1, 0. Column four entries are 0, 0, 0, 1.
Figure 10 - a column major display matrix that flips the y-axis

3. Make the display matrix row major

Take the transpose of both sides of the equation from Figure 9, then rewrite the equation to use the transpose of the display matrix from step 2 above:

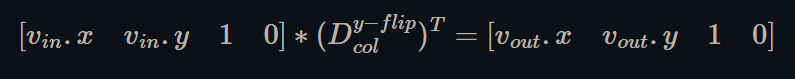
Figure 11. A vector-matrix multiplication equation. It is a 1 by 4 row vector times a 4 by 4 matrix, which equals another 1 by 4 row vector. The components of the first 1 by 4 row vector are "v in dot x", "v in dot y", 1, 0. The 4 by 4 matrix is the transpose of the matrix called "D col y-flip" defined in Figure 10. The components of the second 1 by 4 row vector are "v out dot x", "v out dot y", 1, 0
Figure 11 - rewrite the equation in Figure 9 to use a row major display matrix that flips the y-axis

Therefore, as expressed in Figure 1, the correct, row-major display matrix that flips the y-axis is defined as:

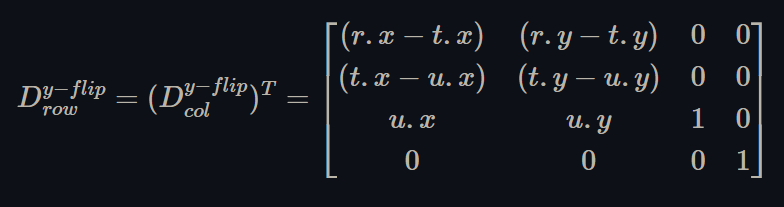
Figure 12. The transpose of the matrix called "D col y-flip," defined in Figure 10, is a row major display matrix that flips the y-axis, called "D row y-flip". It is the same matrix described in Figure 1
Figure 12 - our result, a row major display matrix that flips the y-axis